√70以上 x^2 y^2-z^2=0 313210-X 2 y 2 z 2 2xyz 1
Rotations about the x, y, zaxes of the Bloch sphere are represented by the rotation operator gates Quantum logic gates are represented by unitary matrices A gate which acts on n {\displaystyle n} qubits is represented by a 2 n × 2 n {\displaystyle 2^{n}\times 2^{n}} unitary matrix, and the set of all such gates with the group operation ofZ 2 0 (12r3 − 3r5)dr = 32π (b) F(x,y,z) = (x 2 sin(yz))i (y − xe−z)j z k;If z 2 2z 2 = 0 then both x y2 2x 2 = 0 and 2xy 2y = 0 We begin with the equation from the imaginary part 2xy 2y = 0 2y(x 1) = 0 2y = 0 or x 1 = 0 y = 0 or x = 1 If y = 0, then x2 22x 2 = 0 which has no real solutions (the discriminant b 4ac = ( 2)2 4(1)(2) = 4) Since x is assumed to be real, no solutions result from y = 0

The Divergence Theorem Page 2
X 2 y 2 z 2 2xyz 1
X 2 y 2 z 2 2xyz 1-Transcribed image text Evaluate tripleintegral_B e (x^2 y^2 z^2)^3/2 where B is the ball B = { (x, y, z) x^2 y^2 z^2 lessthanorequalto 16} SOLUTION Since the boundary of B is a sphere, we use spherical coordinates B = { (rho, theta, phi) 0 lessthanorequalto rho lessthanorequalto 4,0 lessthanorequalto theta lessthanorequalto 2 piAnswer to Find the volume of the given solid Enclosed by the paraboloid z = 3x^2 2y^2 and the planes x = 0, y = 2, y = x, z = 0 By signing




Lagrange Multipliers Ppt Download
Solution to Problem Set #9 1 Find the area of the following surface (a) (15 pts) The part of the paraboloid z = 9 ¡ x2 ¡ y2 that lies above the x¡y plane ±4 ±2 0 2 4 x ±4 ±2 0 2 4 y ±4 ±2 0 2 4 Solution The part of the paraboloid z = 9¡x2 ¡y2 that lies above the x¡y plane must satisfy z = 9¡x2 ¡y2 ‚ 0 Thus x2 y2 • 9 We3i Symmetric equations x 1 1 = y5 2 = z 6 3 (b)Find the points in which the required line in part (a) intersects the coordinate planes z= 0 ) x 1 1 = y5 2 = 6 3 = 2 )x= 1;y= 1Example 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the first
Find the work done by the force field F(x, y, z) = (x{eq}^2 {/eq};2 Determine the area bounded by the curves f(x) = 4x and g(x) = 3x1 Answer Z 1 0 (3x1− 4x)dx = 3 2 x2 x− 1 ln4 4x 1 = 5 2 − 3 ln4 3 Determine the area bounded by the xaxis, the yaxis, the line y = 3 and the curveZ) of a moving object along the line segment from A(0, 1, 2) to B(1, 0, 2)
Piece of cake Unlock StepbyStep Natural LanguageClick here👆to get an answer to your question ️ If x^2 = y z, y^2 = z x, z^2 = x y , then the value of 1x 1 1y 1 1z 1 isAlso, I used your technique to get the traces for the surface z=y^2x^2 See the update in my original post $\endgroup$ –



C5




How Do You Find The Volume Of A Solid Where X 2 Y 2 Z 2 9 Is Bounded In Between The Two Planes Z 2x 2 And Z 2x 3 Socratic
Neitherwaseven x=2h1and y=2k1 Then z 2=4h 4h14k2 4k1=4(h hk2 k)2 Thissaysthat2z2 but4 ∤ z2 whichisimpossiblebecause z2 isaperfectsquare Weshallchoose xtobeeven Theorem The triple (x,y,z) is a primitive Pythagorean triple if and only if there existtworelativeprimeintegers sand tsothat s > t >0and x=2st y= s2 −t2 and z= s2 t2S is the surface of the region bounded by the cylinder x2 y2 = 4 and the planes x z = 2 and z = 0 Solution The divergence of F is divF = ∂ ∂x (x2 sin(yz)) ∂ ∂y (y − xe−z) ∂ ∂z (z2) = 2x 12z Let E be the region {(x,y,z) 0 ≤ zZ 2 q 1−x2−y 2 9 0 f(x,y,z)dzdydx Treating S as a x simple region, we have for fixed y − z, x going from 0 to q 1− y2 9 − z2 4 The projected region in the y−z plane can be described as a zsimple region in the y − z plane and described by ((y,z) 0 ≤ z ≤ 2 r 1− y2 9,0 ≤ y ≤ 3) So, the above integral is the same as Z 3
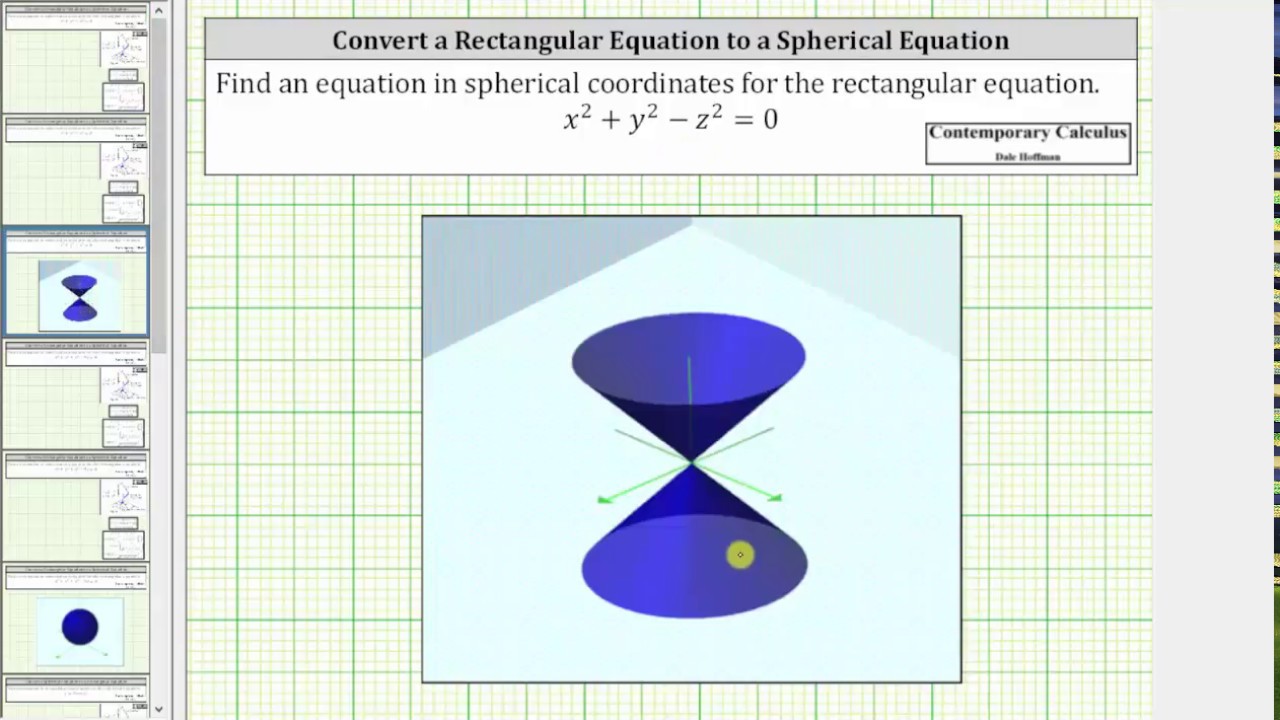



Convert A Rectangular Equation To A Spherical Equation X 2 Y 2 Z 2 0 Youtube



35 Reduce The Equation X 2 Y 2 Z 2 4x 2y 2z 4 0 To One Of The Standard Forms Classify The Surface And Sketch It Toughstem
Winter 12 Math 255 Solution Z C xe 2xdx (x4 2x2y2)dy = Z C Pdx Qdy = ZZ R @Q @x @P @y dA = ZZ R (4x3 4xy2)dA Z 2ˇ 0 Z 2 1 (4r3cos3 4r3cos sin2 )rdrd = 4 Z 2ˇ 0 Z 2 1 (cos3 cos sin2 )r4drd = 4 Z 2ˇ 0 cos d Z 2 1 r4dr = 0 13) Use Green's Theorem to nd the counterclockwisePlot x^2 3y^2 z^2 = 1 Natural Language;Answer (1 of 4) xyzt 16 = 121 Solution below (x1) ^2 (y3) ^2 (z5) ^2 (t7) ^2 = 0 assuming x, y, z, t ∈ R this can be rewritten in the form a^2 b^2 c^2 d^2 = 0 where, a = (x1) b = (y3) c = (z5) d = (t7) for real numbers, a^2 >= 0 b^2 >= 0 c^2 >= 0 d^2 >= 0 In other



16 6e Exercises For Section 16 6 Mathematics Libretexts



If U 2 1 X 2 Y 2 Z 2 Then Show That 2u X 2 2u Y 2 2u Z 2 0 Sarthaks Econnect Largest Online Education Community
OK, here's the solution for Diophantus's problem of determining the solution for x 2 y 2 = z 2 (1) We know that we can assume that x,y,z are coprime See my previous blog for details (2) The second important insight is that z has to be odd (a) Assume the opposite that z is even (b) Then, there exists another value Z such that z = 2 * Z (c) Also, z 2 is then divisible by 4Algebra Examples Rewrite (xy z)2 ( x y z) 2 as (xyz)(xyz) ( x y z) ( x y z) Expand (xyz)(xyz) ( x y z) ( x y z) by multiplying each term in the first expression by each term in the second expression Simplify each term Tap for more steps Multiply x x by x x Multiply y y by y y So substituting the values for the elementary symmetric polynomials that we found, we find that x, y and z are the three roots of t3 −t2 − 1 2t − 1 6 = 0 or if you prefer 6t3 − 6t2 −3t −1 = 0 In theory we could solve this using Cardano's method and directly evaluate x4 y4 z4, but the methods used above are somewhat easier




Example 27 Find Equation Of Plane That Contains The Point 1 1 2
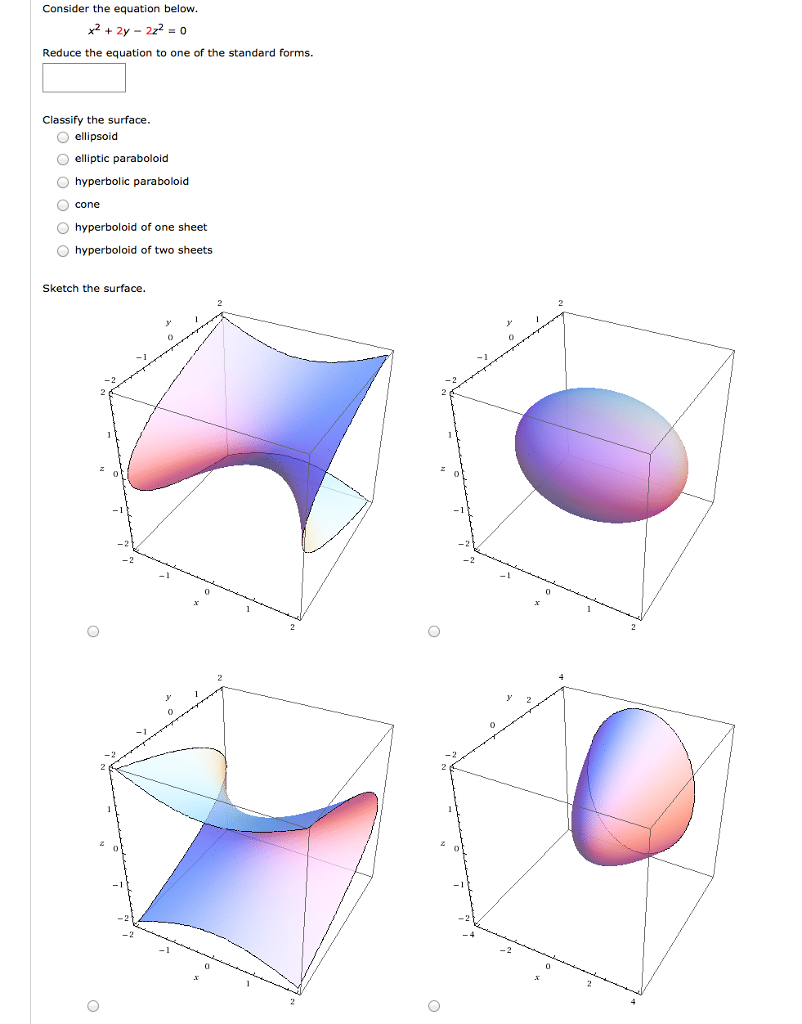



Solved Consider The Equation Below X 2 2y 2z 2 0 Chegg Com
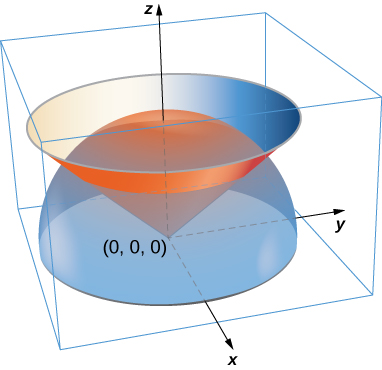
Z V ∇·D d V = Z 2 x=0 Z 2 y=0 Z 2 z=0 0 dx dy dz =0 (c) Apply Gauss' law to calculate the total charge from Eq (429) Q = ♥ Z D·ds =F front F back F right F left F top F bottom, F front = Z 2 y=0 Z 2 z=0 (xˆ2(xy)yˆ(3x−2y)) ¯ ¯ ¯ ¯ ¯ x=2 ·(xˆ dz dy) = Z 2 y=0 Z 2 z=0 2(xy) ¯ ¯ ¯ ¯ ¯ x=2Consider the equation below x 2 − y 2 z 2 − 2x 2y 4z 2 = 0 Reduce the equation to one of the standard forms11 Let Q be the region between z = (x2 y2)3/2 and z = 1, and inside x2 y2 = 4 Sketch the region Q, and then write ZZZ Q p x2 y2ez dV as an integral in the best(for this example) 3dimensional coordinate system DO NOT EVALUATE THE INTEGRAL z = r3 1 1 8 2 z x y Given the form of the solid region and the function, cylindrical coordiates is the best system to use to




How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange



2
2x2yz = 1 First we rearrange the equation of the surface into the form f(x,y,z)=0 z=x^22xyy^2 x^22xyy^2z = 0 And so we define our surface function, f, by f(x,y,z) = x^22xyy^2z In order to find the normal at any particular point in vector space we use the Del, or gradient operator grad f(x,y,z) = (partial f)/(partial x) hat(i) (partial f)/(partial y) hat(j) (partialFrom ∂z/∂x = −ysin(x−y) and ∂z/∂y = cos(x−y)ysin(x−y), it follows that ∂z/∂x(2,2) = 0, ∂z/∂y(2,2) = 1, and hence the tangent plane to z = ycos(x−y) at (2,2,2) is given by z−2 = 0·(x−2)1·(y−2) or, equivalently, y = z Exc The (first) partial derivatives of f(x,y) =X2yz=0, 2xyz=1, 3xy2z=5 \square!




A Sketch And Identify The Type Of Quadric Surface Represented By The Equation Homeworklib




Solve The System Of Equations 3x 3y 2z 1 X 2y 4 10y 3z 2 And 2x 3y Z 5 Answer Mathematics 1 Question Answer Collection
The gray plane is the plane ( x, y) You can see that it is a cone noting that for any y = a the projection of the surface on the plane ( x, z) is a circumference of radius a with equation z 2 x 2 = a 2 Note that z = y 2 − x 2 is the semicone with z > 0, ie above the plane ( x, y) and z = − y 2 − x 2 is the semicone below this planeA sphere is the graph of an equation of the form x 2 y 2 z 2 = p 2 for some real number p The radius of the sphere is p (see the figure below) Ellipsoids are the graphs of equations of the form ax 2 by 2 c z 2 = p 2 , where a , b , and c are all positive2y x = 0 , so that x = 2y Substituting this into the original equation x 2 xy y 2 = 3 leads to (2y) 2 (2y) y y 2 = 3 , 4 y 2 2y 2 y 2 = 3 , 3y 2 = 3 , y 2 = 1 , and Thus, the maximum value of x occurs when y=1 and x=2 , ie, at the point (2, 1) The minimum value of x occurs when y=1 and x=2 , which occurs at the point (2




John Lesieutre Multiplicities




X 2 Y 2 1 0 Chaimmy
Solve the first two for z x²y=z y²x=z x²y = y²x, since both equal to z x²y² = xy (xy)(xy) = (xy) We will see if we can divide by xy We will first assume xy ≠ 0 Then we can divide both sides by xy and get xy = 1 But since z²=xy, then that would mean z²=1 and z would be ±iTrized by x= t, y= t2, 0 t 1 Thus Z C 1 2xds = Z 1 0 2t p 1 4t2dt = 5 p 5 1 6 2 To evaluate R C 2 2xds;we need to parametrize C 2 A vertical line between the given points can be parametrized by x= 1, y= t, 1 t 2 Thus Z C 2 2xds = Z 2 1 2 p 1dt = 2 3 Therefore Z C 2xds= 5 p 5 1 6 2 Two other integrals can be obtained using a similarX 2 1 = y 1 1 = z 1 or x 2 = 1 y= z (a)Find symmetric equations for the line that passes through the point (1;
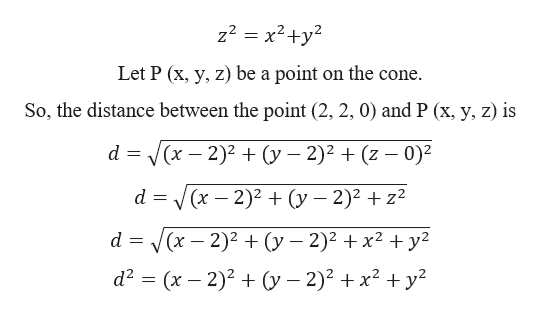



Answered Find The Points On The Cone Z2 X2 Bartleby



2
For the z, direction, it's clearly between z= 0 and z= x2 y2 The double integral formulation is ZZ R (x2 y2 0)dA The triple integral formulation is ZZZ T dV = Z 1 y= 1 Z x=1 2y x=y 1 Z x y2 0 dzdxdy 3Evaluate the volume bounded by the paraboloid z= x2 y2 and the plane z= y 2 This problem is tricky It's on the book It's one Theorem The positive primitive solutions of x^2 y^2 = z^2 with y even are x = r^2 s^2, y = 2rs, z = r^2 s^2, where r and s are arbitrary integers of opposite parity with r>s>0 and gcd(r,s)=1 Using this theorem, find all solutions of the equation x^2 y^2 = 2z^2 (hint write theFall 13 S Jamshidi 4 x4 y4 z4 =1 If x,y,z are nonzero, then we can consider Therefore, we have the following equations 1 1=2x2 2 1=2y2 3 1=2z2 4 x4 y4 z4 =1 Remember, we can only make this simplification if all the variables are nonzero!



Surface Integrals
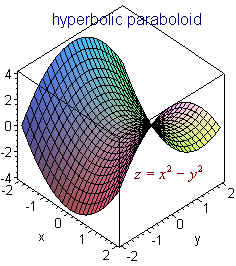



Surfaces
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us! For $x\in\mathbb F_p$ let $S(x)=\{\,(y,z)\in\mathbb F_p^2x^2y^2z^2=0\,\} $ and let $f(x)=S(x)$ Similarly, let $g(x,y)$ the number of $z$ with $x^2y^2z^2=0$ Then $g(x,y)\in\{0,1,2\}$ and $$\tag1f(x)=\left\{\,yg(x,y)=1\,\}\right2\left\{\,yg(x,y)=2\,\}\right$$ Note that $g(x,y)=1$ occurs only if $x^2y^2=0$5;6) and is parallel to the vector h 1;2;



If X 2 Y 2 Z 2 2 X Y Z 3 What Is The Value Of 2x 3y 4z Quora




Lagrange Multipliers Ppt Download
Take the square root of both sides of the equation y^{2}x^{2}z^{2}=0 Quadratic equations like this one, with an x^{2} term but no x term, can still be solved using the quadratic formula, \frac{b±\sqrt{b^{2}4ac}}{2a}, once they are put in standard form ax^{2}bxc=0This is a solution in implicit form We have vertical tangent lines where y = 0 and y = 2, so we can find the corresponding x values 0 = x3 x−2 By inspection, x = 1 (See Maple to get the full set of solutions) If y = 2, then −4 = x3 x−2, or 0 = x3 x2, and by inspection, x = −1The Solution (x2)^2 (y1)^2 (z1)^2 = 0 An Elliptical Cone Reduce the equation to one of the standard forms, classify the surface, and sketch it x^2 y^2 z^2 4x 2y 2z 4 = 0 1) Reorganize the equation x^2 y^2 z^2 4x 2y 2z 4 = 0 >> x^2 4x y^2 2y z^2 2z 4 = 0 2) complete the square




If X Y Z Are Not Equal And X 2 Yz A Y 2 Zx B Z 2
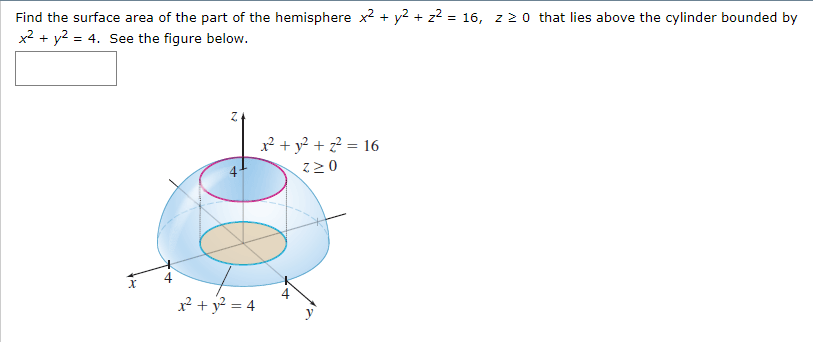



Solved Find The Surface Area Of The Part Of The Hemisphere Chegg Com
Consider the paraboloid z = x2 y2 (a) Compute equations for the traces in the z = 0, z = 1, z = 2, and z = 3 planes Plane Trace z = 0 Point (0;0) z = 1 Circle x2 y = 1 z = 2 Circle x2 y = 2 z = 3 Circle x2 y2= 3 (b) Sketch all the traces that you found in part (a) on the same coordinate axesExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music"The value of `(x^2(yz)^2)/((xz)^2y^2)(y^2(xz)^2)/((xy)^2z^2)(z^2(xy)^2)/((yz)^2x^2)`is`1`(b) 0 (c) 1 (d) None of these"




Engineering Mathematics 233 Solutions Double And Triple Integrals



If X 2 Y 2 Z 2 2xyz 1 Then Prove That Dx 1 X 2 Dy 1 Y 2 Dz 1 Z 2 0 Sarthaks Econnect Largest Online Education Community
X = y = z > x^2 2x = 0 > x(x 2) = 0 then either x = 0 or x = 2 To summarize, the given system of equations have 2 solutions namely (x , y , z) = (0 , 0 , 0) or (x, y , z) =(2 , 2 , 2) If (x , y , z) = (0 , 0 , 0) Then E = 3Prove that if x, y, and z are real numbers such that x^2(yz)y^2(zx)z^2(xy)=0, then at least two of them are equal https//mathstackexchangecom/questions//provethatifxyandzarerealnumberssuchthatx2yzy2zxz The problem is I have to find all the possible combination of integers (x, y, z) that will satisfy the equation x^2 y^2 z^2 = N when you are given an integer N You have to find all the unique tuples (x, y, z) For example, if one of the tuple is




X2 Y2 Z2 1 Geogebra




The Divergence Theorem Page 2
Then the MeshFunctions>{Functionx,y,z, z(4x^2y^2)} Sketch all the points on each plane that satisfies z(4x^2y^2)=0 Have I got that correct?Math 9 Assignment 1 Solutions 2 4 Find the limit if it exists, or show that the limit does not exist lim (x;y)!(0;0) x2 y2 p x2 y2 Solution Notice the following inequality 0 6Z=x^2y^2 WolframAlpha Volume of a cylinder?




Vector Analysis By Alimkanwalimtinaa Issuu



2
Plane between the curves y= x2 y= p xand below the plane z= x y Hence we get Z Z Z xydV = Z 1 0 Zp x x2 Z xy 0 xydzdvdx= Z 1 0 Zp x x2 (xyxy2)dydx This equals 3=28 Section 168 6) Find the volume of the solid that lies between the paraboloid z= x2y2 and the sphere x2y2z2 = 2 Solution In cylindrical coordinates Eis bounded below by theSubstitute (x−2)2 − 4 ( x 2) 2 4 for x2 −4x x 2 4 x in the equation x2 y2 −4x = 0 x 2 y 2 4 x = 0 Move −4 4 to the right side of the equation by adding 4 4 to both sides Add 0 0 and 4 4 This is the form of a circle Use this form to determine the center and radius of the circle



Engineering Purdue Edu
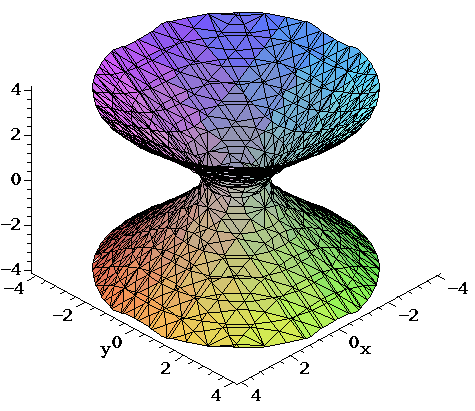



Surfaces Part 2
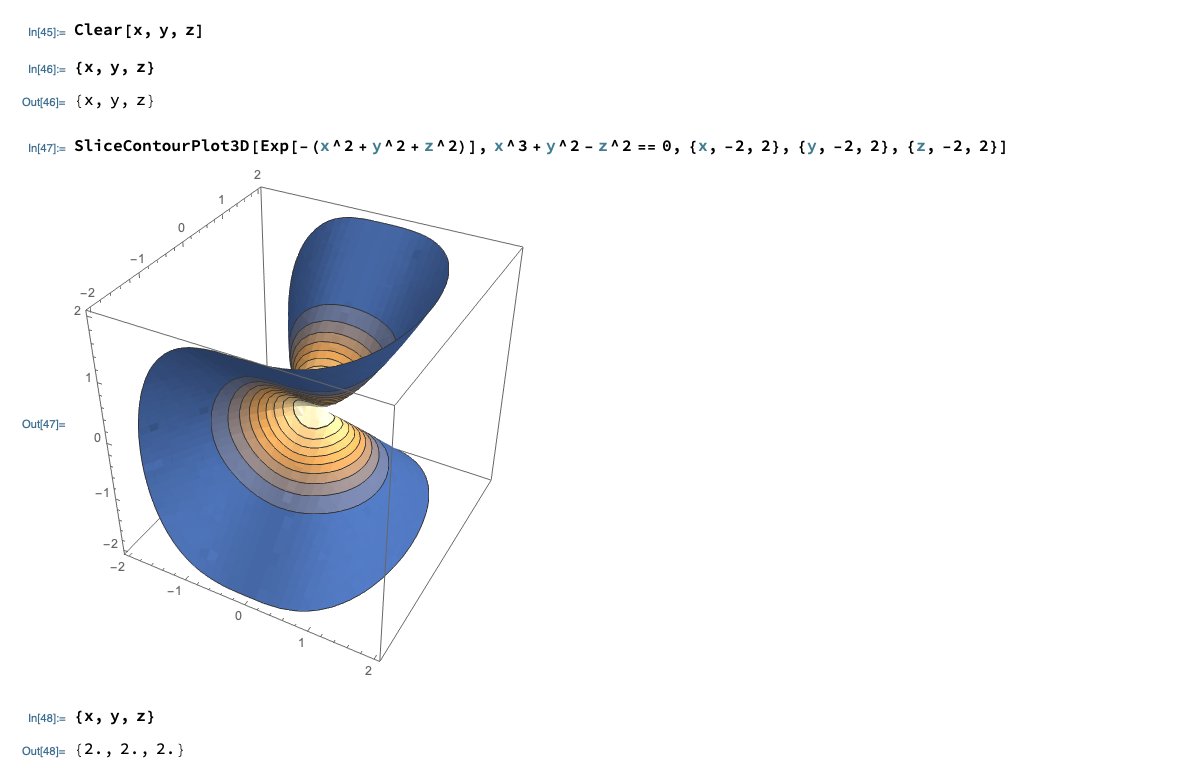



Robert Mcnees Wolframresearch I M Getting The Strangest Bug With Slicecontourplot3d And Slicedensityplot3d After These Commands Are Run The Variables X Y And Z Are Assigned Values X Max Y Max And Z Max




Find The Points On The Cone Z 2 X 2 Y 2 Tat Are Closest To The Point 4 2 0 Youtube



Cmsc 455 Lecture 24b4 Computing Partial Fourth Order Spherical Derivative




Level Surfaces



Solved What Does The Equation X 2 Y 2 Z 2 0 Represent Chegg Com



Surfaces



2



Math Bu Edu



Surfaces




If X X 1 X 2 Represents



1




Plot Of A Portion Of The Variety X 2 Y 2 Z 2 Z 3 0 Download Scientific Diagram




15 8 Triple Integrals In Spherical Coordinates Mathematics Libretexts



2




Solutions For Review Problems



1




Find The Points On The Cone Z 2 X 2 Y 2 That Are Closest Tothe Point 2 2 0 Plainmath




Sphere X 2 Y 2 Z 2 1 Patilksu



2




Se11g01 02 Gif
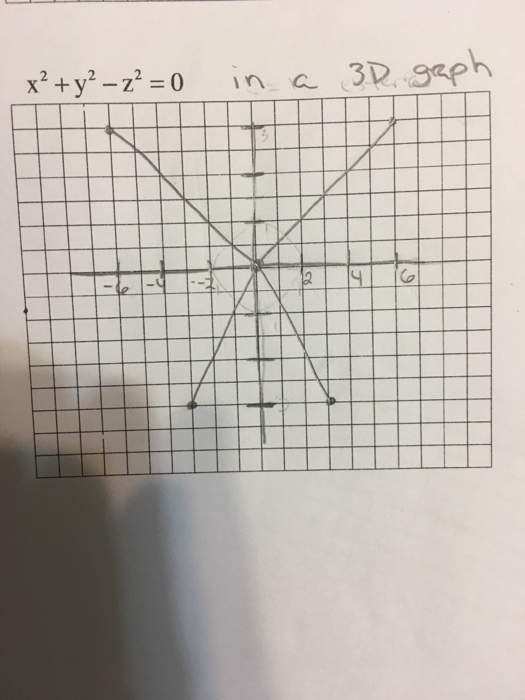



Solved X 2 Y 2 Z 2 0 In A 3d Graph Chegg Com



Solved Consider The Surface Z 2 X 2 Y 2 And The Point P 2 2 0 Find The Points On The Cone That Are Closest To P
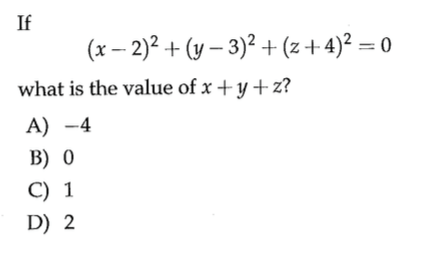



Answered If X 2 2 Y 3 2 Z 4 2 0 What Is The Bartleby
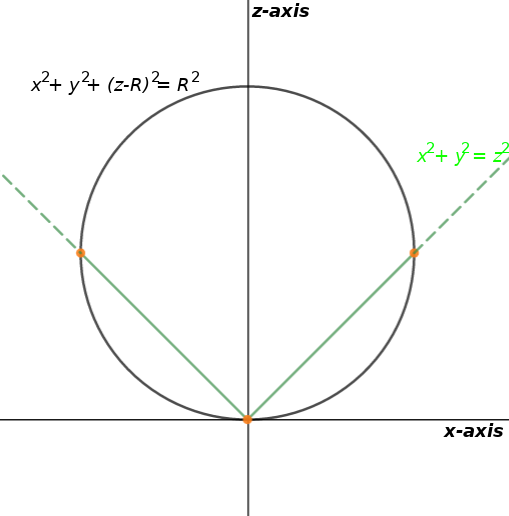



A Compute The Area Of The Portion Of The Cone X 2 Y 2 Quizlet



2




A Sketch And Identify The Surface Z X 2 Y 2 B Find The Equation Of The Intersection Z X 2 Y 2 With Z 5 Sketch And Identify It Study Com



35 Reduce The Equation X 2 Y 2 Z 2 4x 2y 2z 4 0 To One Of The Standard Forms Classify The Surface And Sketch It Toughstem
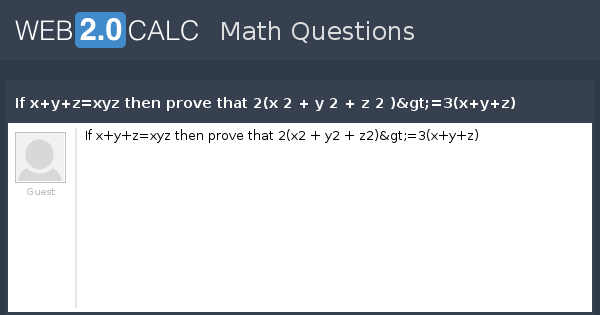



View Question If X Y Z Xyz Then Prove That 2 X 2 Y 2 Z 2 3 X Y Z




Elliptic Paraboloid X 2 Y 2 Z 2 0 Download Scientific Diagram
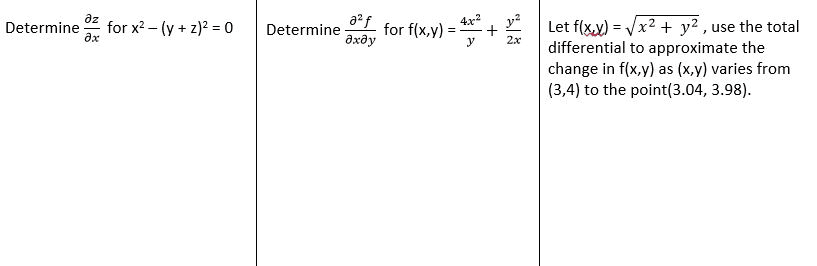



Oneclass Determine Thou Z Thou X For X 2 Y Z 2 0 Determine Thou 2 F Thou X Thou Y For 4 X 2



2




How Do You Solve 2x 9y 2 X 2y 3z 0 And Y Z 1 Using Matrices Socratic




Solve The System Of Equations Re Z 2 0 Z 2
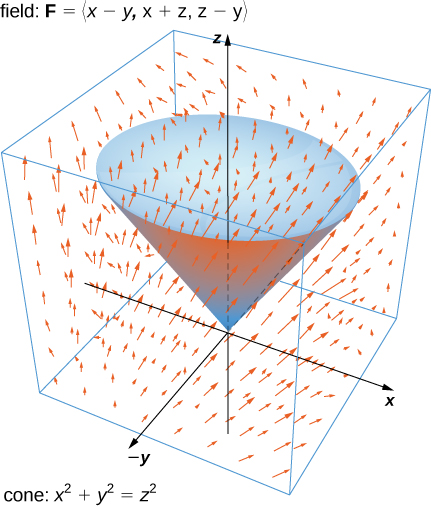



The Divergence Theorem Calculus Volume 3




Setting Up An Integral Over A Solid With Order Of Integration Dr D8 Dz




Assignment 5 Math 215 Q1 1 Evaluate The Triple Integral A



The Point Of Intersection Of The Line Passing Through 0 0 1 And Intersecting The Lines X 2y Z 1 X Y 2z 2 And X Y 2 X Z 2 With Xy Plane Is A Left Frac 5 3 Frac 1 3 0right B 1 1 0 C Left Frac 2 3 Frac 1 3 0right D




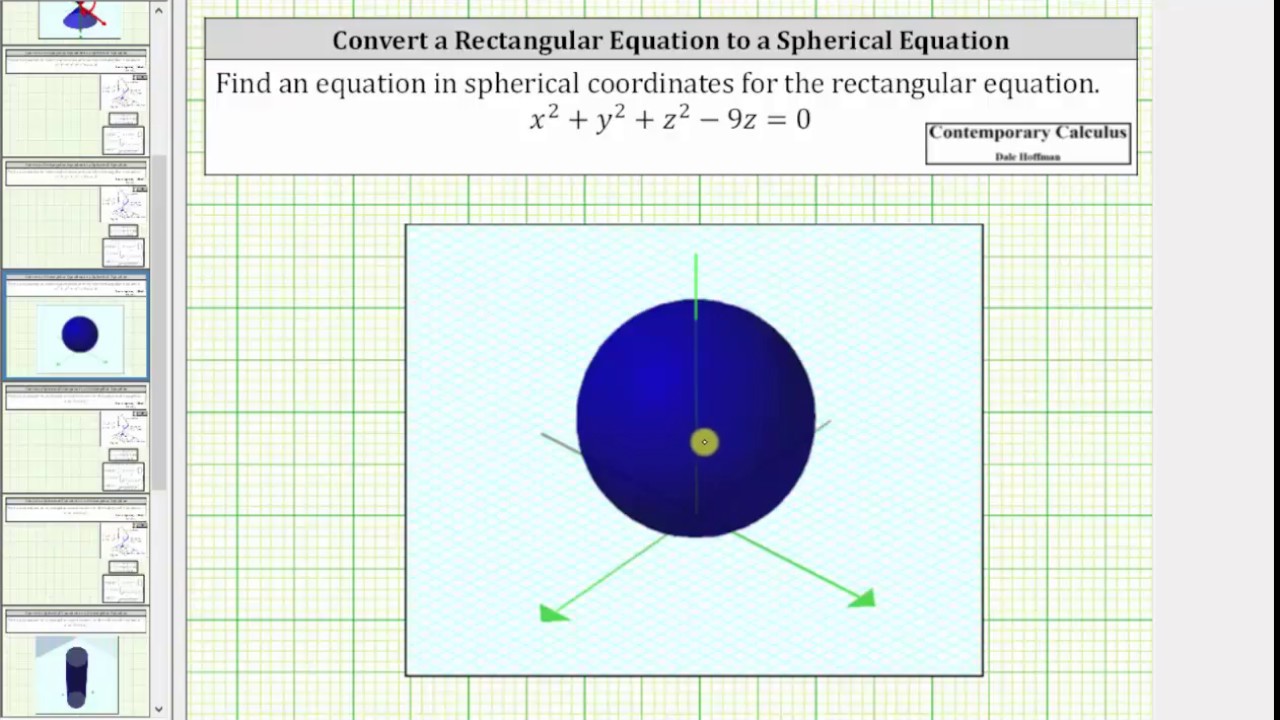
Equation Of The Sphere Is 2x 2 2y 2 2z 2 8x 12y 16z 8 0 Find Its Centre And Radius



Surfaces



What Is The Solution To This System Of Equations Gauthmath



How To Find X In Terms Of Y And X In The Equation X 2 Xy Z 2 0 Quora



Solved Describe The Surface Whose Equation Is Given X 2 Y 2 Z 2 Y 0



2



2




The Surface X 2 Y 2 Z 2 2xy Z A Is Shown In The Case A 0 5 Download Scientific Diagram




If X2 Y2 Z2 2 X Y Z 3 Find The Value Of 2x 3y 4z Brainly In



2




John Lesieutre Base Loci




The Plane X 2y Z 4 Cuts The Sphere X 2 Y 2 Z 2 X Z 2 0 In A Circle Of Radius A 3 B 1 C 2 D Sqrt 2




1 Sketch The Surface Z X 2 Y 2 2 Sketch The Surface Z 2y 2 4x 2 Study Com



2



1




Analytical Geometry Notes



Surface Area



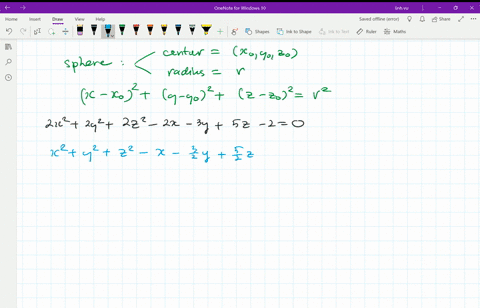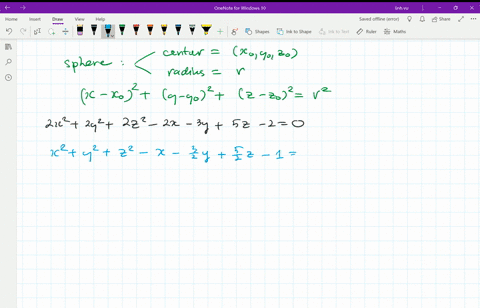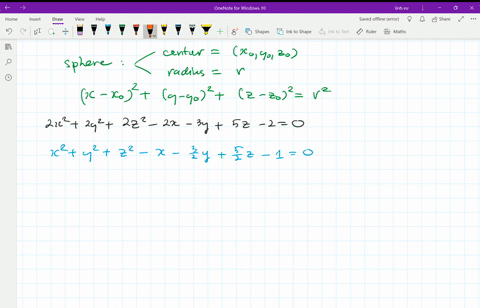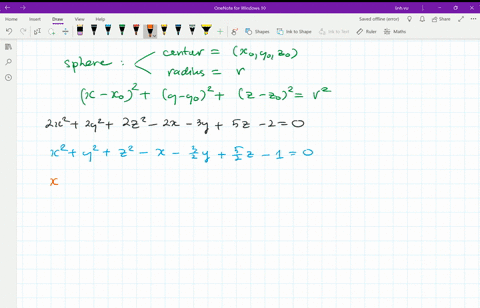
Convert A Rectangular Equation To A Spherical Equation X 2 Y 2 Z 2 9z 0 Youtube




If X2 Y2 Z2 Xy Yz Xx O Prove That X Y Z Maths Polynomials Meritnation Com



Solved A Evaluate The Surface Integral Z V X2 Y2 Ds Where O Is The Surface Of The Sphere X2 Y2 Z2 4 For Z 2 0 B Use Gauss Theorem To Course Hero




How To Plot Z 5 Sqrt X 2 Y 2 0 Le Z Le 5 In Mathematica Mathematics Stack Exchange




How To Plot X 2 Y 2 Z 2 Mathematics Stack Exchange




Homework Assignment 4 Math 253
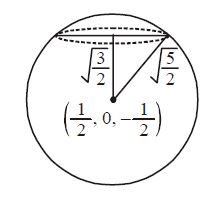



The Plane X 2y Z 4 Cuts The Sphere X2 Y2 Z2 X
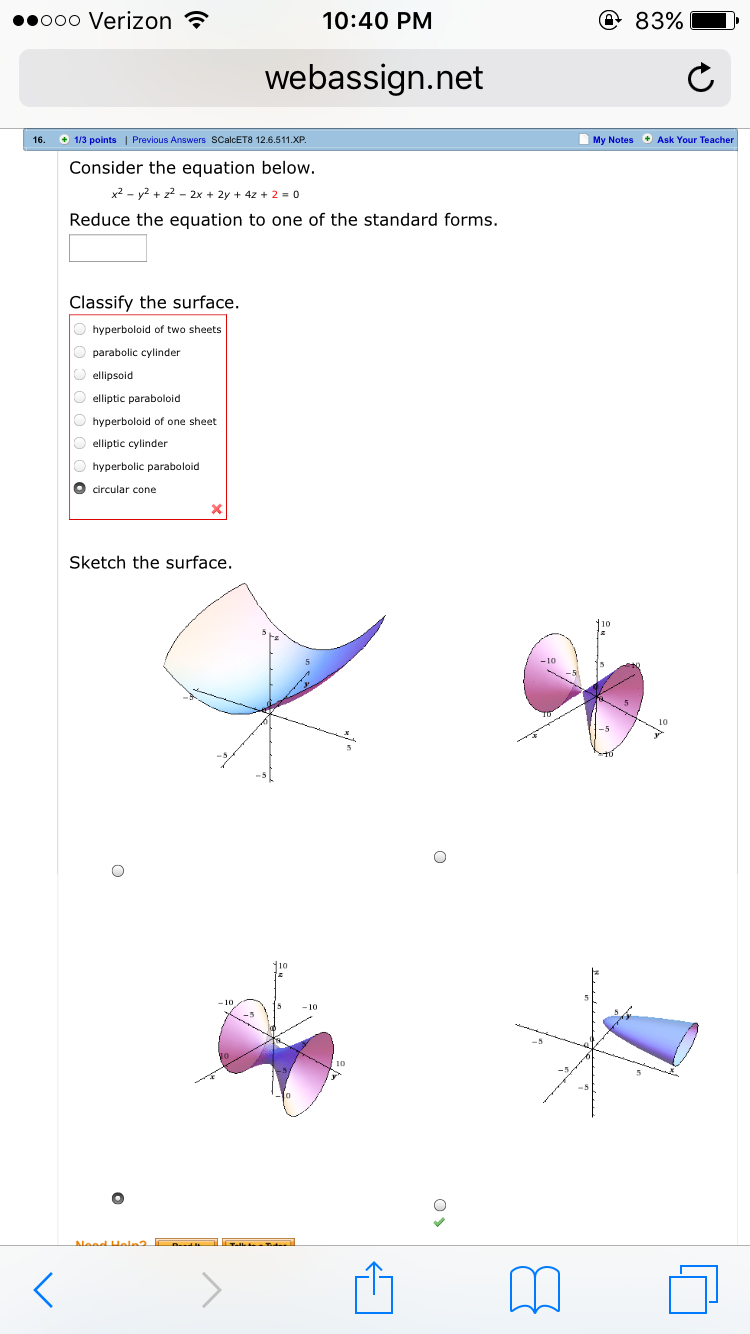



Solved Consider The Equation Below X 2 Y 2 Z 2 2x Chegg Com




Make 2x 2 Y 2 Z 2 X 2 2y 2 Z 2 X 2 Y 2 2z 2 Squares Fun With Num3ers




6 Consider The Sphere S Cut Out By Z2 Y2 22 Maximize Daf P Where Y Z 2y 3z And U Is A Unit Vector In The Tangent Plane To S At



Solved Form Partial Differential Equation By Eliminating The Arbitrary Function F Ax By Cz X 2 Y 2 Z 2 0 Also Find Order And Degree Of The Course Hero




Graphing 3d Graphing X 2 Y 2 Z 2 Intro To Graphing 3d Youtube




Surfaces Part 2




Surfaces Part 2



2



2



Multiple Integrals1 Html




Evaluate Please X 2 Y 2 3 Y 2 Z 2 3 Z 2 X 2 3 Divided By X Y 3 Y Z 3 Z X 3 Brainly In



1



2
コメント
コメントを投稿